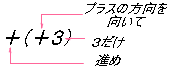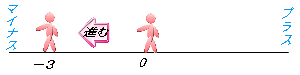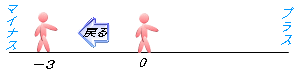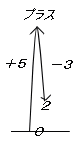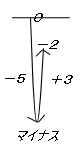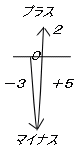�����̐�
�O��菬�������̂�\���Ƃ��A�O���ǂꂾ�������������u�|�v�̕��������ā|�P�A�|�Q�Ȃǂ̂悤�ɕ\���܂��B
�u�|�v�̕����̓}�C�i�X�Ɠǂ݂܂��B
��Βl
�O���ǂꂾ���傫�����A�܂��͏����������Βl�Ƃ����܂��B
�O����ǂꂾ������Ă��邩��\�����߁A��Βl�͂O����̋����Ɖ������Ă��܂��B
�Ⴆ�i�|�R�j�̐�Βl�͂R�ł��B
�����̐��̉����̊�b
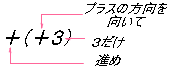 |
 |
�{�R |
 |
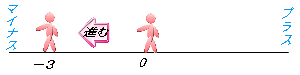 |
�|�R |
 |
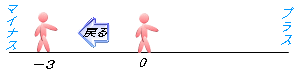 |
�|�R |
�}�C�i�X�̕�����
�R�i�̂Ɠ���
����������
�|�i�{�R�j���{�i�|�R�j
�Ђ��Z�������Z�ɂ��邱�Ƃ��ł��� |
 |
 |
�{�R |
�v���X�̕�����
�R�i�̂Ɠ���
����������
�|�i�|�R�j���{�i�{�R�j
�Ђ��Z�������Z�ɂ��邱�Ƃ��ł��� |
�����̐��̉��@�i�����Z�j
�������̓����Q�̐��̉��@���@�E�E�E�@�i�{���j�{�i�{���j�@�܂��́@�i�|���j�{�i�|���j
�i�{���j�{�i�{���j�@�ŏ��Ɂu�{�v���ȗ�����Ă���ƍl���ā@�{�i�{���j�{�i�{���j
�@�v���X�̕����Ɂ������i��ŁA�v���X�̕����Ɂ������i�ށB
�@���������ăv���X�̕����Ɂi���{���j�i���ƂɂȂ�B
�i�{���j�{�i�{���j���{�i���{���j
�i�|���j�{�i�|���j�@�ŏ��Ɂu�{�v���ȗ�����Ă���ƍl���ā@�{�i�|���j�{�i�|���j
�@�}�C�i�X�̕����Ɂ������i��ŁA�}�C�i�X�̕����Ɂ������i�ށB
�@���������ă}�C�i�X�̕����Ɂi���{���j�i���ƂɂȂ�B
�i�|���j�{�i�|���j���|�i���{���j
|
|
��
�@ |
�i�{�Q�j�{�i�{�R�j |
���{�i�Q�{�R�j
���T |
|
| �i�|�T�j�{�i�|�S�j |
���|�i�T�{�S�j
���|�X |
|
�����̓����Q�̐��̘a�́A
���Ƃ̐��̕��������Ă���
��Βl�̘a�������悢 |
�������̈قȂ�Q�̐��̉��@���@�E�E�E�@�i�{���j�{�i�|���j�@�܂��́@�i�|���j�{�i�{���j
�v���X�̕����Ɂ������i��ŁA�}�C�i�X�̕����Ɂ������i�ށB
�}�C�i�X�̕����Ɂ������i��ŁA�v���X�̕����Ɂ������i�ށB
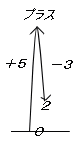 |
�ŏ��ɑ傫���v���X�̕����Ɂ������i�ށB
���ɋt�����Ɂ������i�ށB
�傫���i�ق��̕��������A���������ɂ͐i�����̍�������B
|
|
| �� |
�i�{�S�j�{�i�|�R�j |
���{�i�S�|�R�j
���P |
|
|
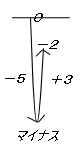 |
�ŏ��ɑ傫���}�C�i�X�̕����Ɂ������i�ށB
���ɋt�����Ɂ������i�ށB
�傫���i�ق��̕��������A���������ɂ͐i�����̍�������B
|
|
| �� |
�i�|�S�j�{�i�{�Q�j |
���|�i�S�|�Q�j
���|�Q |
|
|
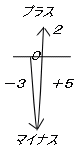 |
�ŏ��ɏ������i�݁A�t�����ɂO���܂����ő傫���i�ތv�Z�́A
����Ȃ������͊ԈႦ�₷���̂ŁE�E�E
�i�{�R�j�{�i�|�T�j���i�|�T�j�{�i�{�R�j�@�܂��́@
�i�|�R�j�{�i�{�T�j���i�{�T�j�{�i�|�R�j�@�̂悤�ɁA
�����Z�̏��Ԃ�ς��čl����悢�B
|
|
| �� |
�i�{�Q�j�{�i�|�R�j |
���i�|�R�j�{�i�{�Q�j
���|�i�R�|�Q�j
���|�P |
|
| �i�|�P�j�{�i�{�S�j |
���i�{�S�j�{�i�|�P�j
���{�i�S�|�P�j
���R |
|
|
�����Ӂ@�����Z�͏��Ԃ�ς��邱�Ƃ��ł���
�����̈قȂ�Q�̐��̘a�́A
��Βl�̑傫�ȕ��̕��������Ă���
��Βl�̍��������悢 |
�����̐��̌��@�i�Ђ��Z�j
�Ђ��Z�͕K�������Z�ɒ����Ă���v�Z���܂��B
|
|
��
�A |
�i�|�T�j�|�i�{�R�j |
���i�|�T�j�{�i�|�R�j
���|�i�T�{�R�j
���|�W |
|
| �i�|�T�j�|�i�|�R�j |
���i�|�T�j�{�i�{�R�j
���|�i�T�|�R�j
���|�Q |
|
���̐������������Z�E�Ђ��Z
�܂��A�Ђ��Z�������Z�ɒ����܂��B
���ɁA�����珇�ԂɌv�Z���܂��B�@�E�E�E�i�����Z�ɒ����Ȃ������ꍇ�A���Ԃǂ���Ɍv�Z���Ȃ��Ɠ���������Ă��܂��j
|
|
��
�B
�T |
�i�|�Q�j�|�i�|�R�j�{�i�|�R�j�|�i�{�T�j�{�i�{�S�j |
���i�|�Q�j�{�i�{�R�j�{�i�|�R�j�{�i�|�T�j�{�i�{�S�j
���i�{�P�j�{�i�|�R�j�{�i�|�T�j�{�i�{�S�j
���i�|�Q�j�{�i�|�T�j�{�i�{�S�j
���i�|�V�j�{�i�{�S�j
���|�R |
|
�Ђ��Z�������Z�ɒ�������A�v���X�̂��̂ƃ}�C�i�X�̂��̂��Čv�Z����ƊȒP�ɂł��܂��B
|
|
��
�B
�U |
�i�|�Q�j�|�i�|�R�j�{�i�|�R�j�|�i�{�T�j�{�i�{�S�j |
���i�|�Q�j�{�i�{�R�j�{�i�|�R�j�{�i�|�T�j�{�i�{�S�j
���i�|�Q�j�{�i�|�R�j�{�i�|�T�j�{�i�{�R�j�{�i�{�S�j
���|�i�Q�{�R�{�T�j�{�i�R�{�S�j
���i�|�P�O�j�{�i�{�V�j
���|�R |
�E�E�E�@�܂��́A�����Z�ɒ���
�E�E�E�@���������̂��̂��Ƃɕ�����
�E�E�E�@���������̂��̓��m�v�Z
�@
�@ |
|
���������͂���
�ŏ��ɂ����Z�ɒ����Ă���A�������̊O�ɂ���{�ƁA�����������������B
|
|
��
�C |
�i�|�Q�j�{�i�{�R�j�{�i�|�S�j�|�i�{�T�j�|�i�|�U�j |
���i�|�Q�j�{�i�{�R�j�{�i�|�S�j�{�i�|�T�j�{�i�{�U�j
���|�Q�{�R�|�S�|�T�{�U |
|
���ۂɌv�Z����Ƃ��́u�������v������Ǝv���Čv�Z���܂��B
|
|
| �� |
�i�|�Q�j�{�i�{�R�j�|�i�{�R�j�{�i�|�T�j�|�i�|�S�j |
���i�|�Q�j�{�i�{�R�j�{�i�|�R�j�{�i�|�T�j�{�i�{�S�j
���|�Q�{�R�|�R�|�T�{�S
���|�Q�|�R�|�T�{�R�{�S
���|�i�Q�{�R�{�T�j�{�i�R�{�S�j
���|�P�O�{�V
���|�R |
|
�����̐��̏�@�i�����Z�j
����30m�Ői�Ƃ��A10����A10���O���ꂼ��ǂ��̈ʒu�ɂ��邩�B
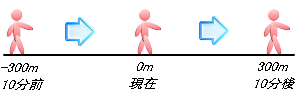
�@10����i�{10���j�@�F�@�i�{300m/���j�~�i�{10���j���{300m�@�E�E�E�@�v���X�~�v���X���v���X
�@10���O�i�|10���j�@�F�@�i�{300m/���j�~�i�|10���j���|300m�@�E�E�E�@�v���X�~�}�C�i�X���}�C�i�X
����30m�Ŗ߂����Ƃ��A10����A10���O���ꂼ��ǂ��̈ʒu�ɂ��邩�B

�@10����i�{10���j�@�F�@�i�|300m/���j�~�i�{10���j���|300m�@�E�E�E�@�}�C�i�X�~�v���X���}�C�i�X
�@10���O�i�|10���j�@�F�@�i�|300m/���j�~�i�|10���j���{300m�@�E�E�E�@�}�C�i�X�~�}�C�i�X���v���X
���̂��Ƃ���A�������킹��Q�̐��̕����ɂ���ē����̕��������܂邱�Ƃ��킩��܂��B
�������̐ς̓v���X
�ٕ����̐ς̓}�C�i�X |
|
|
��
�D |
�i�|�Q�j�~�i�{�R�j |
���|�i�Q�~�R�j
���|�U |
|
| �i�{�S�j�~�i�|�Q�j |
���|�i�S�~�Q�j
���|�W |
|
| �i�|�R�j�~�i�|�T�j |
���{�i�R�~�T�j
���P�T |
|
�t��
�����ĂP�ɂȂ鐔���A���Ƃ̐��̋t���Ƃ����܂��B
| �Q�~ |
�P |
���P�@���������āA�Q�̋t���� |
�P |
�ɂȂ�܂��B |
|
|
| �Q |
�Q |
| �Q |
�~ |
�R |
���P�@���������āA |
�Q |
�̋t���� |
�R |
�ɂȂ�܂��B |
|
|
|
|
| �R |
�Q |
�R |
�Q |
| �i�|�R�j�~�i�| |
�P |
�j���P�@���������āA�|�R�̋t���́| |
�P |
�ɂȂ�܂��B |
|
|
| �R |
�R |
| �Q�������邱�Ƃ� |
�P |
�{���邱�ƂƓ����ł��B�@���������āA���Q���~ |
�P |
�Ɠ������ƂɂȂ�܂��B |
|
|
| �Q |
�Q |
| ���l�Ɂ� |
�Q |
���~ |
�R |
�A�܂��A���i�|�R�j���~�i�| |
�P |
�j�Ɠ������ƂɂȂ�܂��B |
|
|
|
| �R |
�Q |
�R |
���鐔�ł�邱�Ƃ�
���̐��̋t���������邱�ƂƓ��� |
�����̐��̏��@�i���Z�j
���@�̏ꍇ�A�t���̍l�������g���āA�����Z�ɒ����Ă���v�Z���܂��B
|
|
��
�E |
| �i�|�W�j���i�{�R�j |
���i�|�W�j�~�i�{ |
�P |
�j |
|
| �R |
|
|
|
|
| �i�|�P�Q�j���i�|�R�j |
���i�|�P�Q�j�~�i�| |
�P |
�j |
|
| �R |
|
| ���{�i�P�Q�~ |
�P |
�j |
|
| �R |
| ���S |
|
|
|
| �i�{�S�j���i�| |
�Q |
�j |
���i�{�S�j�~�i�| |
�R |
�j |
|
|
| �R |
�Q |
|
| ���|�i�S�~ |
�R |
�j |
|
| �Q |
| ���|�U |
|
|
|
�ݏ�
�ݏ�i�邢���傤�j�͂��̂��̂��������킹�邩��\���Ă��܂��B
�E��ɂ����鐔���ɂ���ĂQ��A�R��ȂǂƂ����܂��B
�Q��̂��Ƃ��i�ւ��ق��j�A�R��̂��Ƃ𗧕��i����ۂ��j�Ƃ����܂��B
���L�̂Q��ނ��o�Ă���̂ŋ�ʂł���悤�ɁB
�^�C�v�P�@�i�|���j���@�̏ꍇ�@�E�E�E�@�������̒��g���������킳�ꂽ����\���܂��B
�i�|�Q�j���Q�����킹��@�E�E�E�@�i�|�Q�j�Q���i�|�Q�j�~�i�|�Q�j���S
�i�|�Q�j���R�����킹��@�E�E�E�@�i�|�Q�j�R���i�|�Q�j�~�i�|�Q�j�~�i�|�Q�j���|�W
�^�C�v�Q�@�|�����@�̏ꍇ�@�E�E�E�@���O�̐��������������킳�ꂽ����\���܂��B
�|�Q�Q���|�i�Q�~�Q�j���|�S
�|�Q�R���|�i�Q�~�Q�~�Q�j���|�W
������Ə����������
�@�|�Q�Q���i�|�P�j�~�Q�Q���|�S
�@�|�Q�R���i�|�P�j�~�Q�R���|�W
�Ƃ����Ӗ��ɂȂ�܂��B
| �i�|���j���Ɓ|�����̈Ⴂ�ɒ��� |
���̐������������Z
�i�|�Q�j���i�|�P�j�~�Q�@�A�܂��A�i�{�Q�j���Q
���ۂɁi�|�P�j�~�Q���v�Z���Ă݂�Ɓi�|�Q�j�ɂȂ邱�Ƃ��킩��͂��B
���̂��Ƃ��g���āA���ɏo�Ă���i�|���j���i�|�P�j�~���ɒ������Ƃ��ł���B
|
|
��
�F |
�i�|�Q�j�~�i�{�R�j�~�i�|�R�j�~�i�{�T�j |
���i�|�P�j�~�Q�~�R�~�i�|�P�j�~�R�~�T
���i�|�P�j�~�i�|�P�j�~�Q�~�R�~�R�~�T�@�E�E�E�@�����Z�͂Ȃ�т������ł��邩��
�������ŁA�i�|�P�j�̕����ƁA����ȊO�̕����ŕ����čl���遄
���i�{�P�j�~�X�O
���X�O
|
|
��̗�łQ�~�R�~�R�~�T���X�O�@�E�E�E�@����͂��Ƃ̐��̂��ꂼ��̐�Βl�̐�
�����Łi�|�P�j�~�i�|�P�j�̕����͉���\���Ă��邩�B
�i�|�P�j���Q�����킹���Ƃ��@�i�|�P�j�~�i�|�P�j���P
�i�|�P�j���R�����킹���Ƃ��@�i�|�P�j�~�i�|�P�j�~�i�|�P�j���|�P
�i�|�P�j���S�����킹���Ƃ��@�i�|�P�j�~�i�|�P�j�~�i�|�P�j�~�i�|�P�j���P |
�E�E�E�v���X
�E�E�E�}�C�i�X
�E�E�E�v���X |
���ۂɌv�Z���Ċm���߂Ă݂܂��傤�B
�i�|�P�j���T��ȏォ�����킹���Ƃ������l�Ɍv�Z���ĕ\�ɂ��Ă݂�ƁA
�i�|�P�j���������킹����
| �P�������킹�� |
�}�C�i�X |
| �Q�������킹�� |
�v���X |
| �R�������킹�� |
�}�C�i�X |
| �S�������킹�� |
�v���X |
| �T�������킹�� |
�}�C�i�X |
| �U�������킹�� |
�v���X |
| �V�������킹�� |
�}�C�i�X |
�i�|�P�j���������킹�����ɂ���ĕ��������܂�܂��B
���������āA��قǂ̗�́i�|�P�j�~�i�|�P�j�̕����œ����̕��������߂��Ă������Ƃ��킩��܂��B
���̏ꍇ�Q�����̂ŁA�����̓}�C�i�X�ɂȂ邱�Ƃ��킩��܂��B
���̒��Ń}�C�i�X��������킳���Γ����̓}�C�i�X
���������킳���Γ����̓v���X |
�����Ӂ��@��E�������Ċo���Ă܂����H
�@��͂P�C�R�C�T�C�V�Ȃǁi�Q�ł��ƂP�]�鐔�j
�@�����͂Q�C�S�C�U�C�W�Ȃǁi�Q�ł�肫��鐔�j
���̐������������Z�̏ꍇ�A
�}�C�i�X�̍��̐��Ŕ��f����镄�������Ă���
�e���̐�Βl�̐ς������悢 |
|
|
��
�G |
�i�|�Q�j�~�i�{�R�j�~�i�|�Q�j�~�i�|�S�j |
���i�|�P�j�~�Q�~�R�~�i�|�P�j�~�Q�~�i�|�P�j�~�S
���i�|�P�j�~�i�|�P�j�~�i�|�P�j�~�Q�~�R�~�Q�~�S
���i�|�P�j�~�S�W
���|�S�W
|
�@
�E�E�E�@�����Z�͂Ȃ�т������ł��邩��
�E�E�E�@�i�|�P�j���R������
�@ |
|
��@�Ə��@�����������v�Z
���@�̏ꍇ�A���Z�͂����Z�ɒ����Ă���v�Z���邱�Ƃ��o����ׁA
�����̕����̌��ߕ��͏�@�Ƃ܂����������ł��B
�K����x�����Z�ɒ����Ă���v�Z���܂��傤�B
�l�������Z
�����Z�E���Z���ɁA�����Z�E�Ђ��Z����Ɍv�Z���܂��B
|
|
��
�H
�T |
�i�|�Q�j�{�i�{�R�j�~�i�|�S�j�|�i�{�T�j |
���i�|�Q�j�{�i�|�P�Q�j�|�i�{�T�j
���i�|�Q�j�{�i�|�P�Q�j�{�i�|�T�j
���|�i�Q�{�P�Q�{�T�j
���|�P�X |
�E�E�E�܂��͂����Z�����Ɍv�Z
�E�E�E�Ђ��Z�������Z�ɒ���
�@
�@ |
|
�ݏ�́A�����Z�E���Z������Ɍv�Z���܂��B
|
|
��
�H
�U |
�i�|�P�j�{�i�|�R�j�~�i�|�Q�j�Q�|�i�|�S�j |
���i�|�P�j�{�i�|�R�j�~�i�{�S�j�|�i�|�S�j
���i�|�P�j�{�i�|�P�Q�j�|�i�|�S�j
���i�|�P�j�{�i�|�P�Q�j�{�i�{�S�j
���|�i�P�{�P�Q�j�{�i�{�S�j
���i�|�P�R�j�{�i�{�S�j
���|�X |
�E�E�E�ݏ悪�ŗD��
�E�E�E�����Z�����Ɍv�Z
�E�E�E�Ђ��Z�������Z�ɒ���
�@
�@
�@ |
|
|
|
��
�H
�V |
�i�|�R�j�|�i�|�Q�j�Q�{�i�|�S�j |
���i�|�R�j�|�i�{�S�j�{�i�|�S�j
���i�|�R�j�{�i�|�S�j�{�i�|�S�j
���|�i�R�{�S�{�S�j
���|�P�P |
�E�E�E�ݏ悪�ŗD��
�E�E�E�Ђ��Z�������Z�ɒ���
�@
�@ |
|
|
|
��
�H
�W |
�T�|�Q�Q�~�R�|�P�{�S |
���T�|�S�~�R�|�P�{�S
���T�|�P�Q�|�P�{�S
���T�{�S�|�P�Q�|�P
���X�|�P�R
���|�S |
�E�E�E�ݏ悪�ŗD��
�E�E�E�����Z�����Ɍv�Z
�E�E�E�@�v���X�̂��̂ƃ}�C�i�X�̂��̂���
�@
�@ |
|
�������̂���ꍇ�A�������̒�������ɁA�l�������v�Z�̎菇�ɂ��������Čv�Z���܂��B
�o�p�͒��������Ƃ����܂��B
|
|
��
�H
�X |
�i�|�R�j�~�o�i�|�T�j�{�i�{�S�j���i�|�Q�j�p�{�i�|�V�j |
���i�|�R�j�~�o�i�|�T�j�{�i�|�Q�j�p�{�i�|�V�j
���i�|�R�j�~�o�i�|�V�j�p�{�i�|�V�j�@
���i�|�R�j�~�i�|�V�j�{�i�|�V�j
���i�{�Q�P�j�{�i�|�V�j
���P�S |
�E�E�E���������̒����l�������v�Z��
�@�@�@�菇�ɂ��������Čv�Z
�E�E�E���������̒��g�̌v�Z���I��
�E�E�E��������������
�E�E�E�l�������v�Z�̎菇��
�@�@�@���������Čv�Z�@ |
|
|
|
��
�H
�Y |
�|�R�Q�{�i�|�Q�~�R�|�Q�R�j���Q |
���|�R�Q�{�i�|�Q�~�R�|�W�j���Q
���|�R�Q�{�i�|�U�|�W�j���Q
���|�R�Q�{�i�|�P�S�j���Q
���|�R�Q�|�P�S���Q
���|�X�|�P�S���Q
���|�X�|�V
���|�P�U |
�E�E�E�������̒����l�������v�Z��
�@�@�@�菇�ɂ��������Čv�Z
�E�E�E�������̒��g�̌v�Z���I��
�E�E�E������������
�E�E�E�l�������v�Z�̎菇�ɂ��������Čv�Z
�@
�@ |
|
�����̐����g�������ۂ̗�
�S���t�̃X�R�A���v�Z���鎞
�S���t�ł́A�ЂƂ̃z�[�����ƂɊ�ƂȂ�Ő������߂��Ă��܂��B
�R�łŃ{�[�����J�b�v�ɓ��邱�Ƃ���ɂȂ��Ă���ꍇ�A�p�[�R�A
�S�łŃ{�[�����J�b�v�ɓ��邱�Ƃ���ɂȂ��Ă���ꍇ�A�p�[�S�Ȃǂ̂悤�ɏ�����Ă��܂��B
��������Ƃɂ��āA��ɂȂ��Ă���Ő��Ń{�[�����J�b�v�ɓ������ꍇ�A�X�R�A�͂O
��ɂȂ��Ă���Ő������P�ő����������Ă��܂����ꍇ�A�X�R�A�́{�P
��ɂȂ��Ă���Ő������Q�ő����������Ă��܂����ꍇ�A�X�R�A�́{�Q
��ɂȂ��Ă���Ő������P�ŏ��Ȃ��ă{�[�����J�b�v�ɓ������ꍇ�A�X�R�A�́|�P
�܂�A�X�R�A�͑S�Đ����̐��ŕ\����A�}�C�i�X�ɂȂ�قǐ��т��ǂ��Ƃ������ƂɂȂ�܂��B
�����̃X�R�A�����Ă����A�Ō�ɐ����̐��̂����Z�����č��v�̐��т����܂��B
|
�Pΰ� |
�Qΰ� |
�Rΰ� |
�Sΰ� |
�Tΰ� |
�Uΰ� |
�Vΰ� |
�Wΰ� |
�Xΰ� |
���v�X�R�A |
| A���� |
�O |
�{�P |
�O |
�O |
�|�P |
�|�P |
�O |
�{�P |
�{�P |
�{�P |
| B���� |
�|�P |
�O |
�O |
�|�P |
�O |
�{�Q |
�{�P |
�O |
�|�P |
�O |
�����̐��̂����Z�ɂ���āAB����̕������v�X�R�A���ǂ��i�Ő������Ȃ��j���Ƃ��킩��܂���
�����̐����g�����֗��Ȍv�Z�i���v�j
��������98�~�̃m�[�g�U���ƁA105�~�̃y�����Q�{�������ꍇ�̍��v���z
�Q��ނ̕i���̒l�i��98�~��105�~�Ȃ̂ŁA���̊Ԃɂ��鐔���Ōv�Z���₷�����Ȑ����́E�E�E100
100�~����ɍl���āA�m�[�g�U���ƃy���Q�{�ō��v�W�̕i����������A
100�~�~�W��800�~
���v���z��800�~���炢�ɂȂ�Ɨ\�z�ł���i��̐����̍��v�j
100�~����ɂ��Ă��ꂼ��̕i���̒l�i�𐳕��̐����g���ĕ\���Ă݂��
�m�[�g�͊��100�~���Q�~��������i�|�Q�j
�y���͊��100�~���T�~��������i�{�T�j
�Q�~�������̂��U�ƁA�T�~�������̂��Q����������
�@ �i�|�Q�j�~�U�{�i�{�T�j�~�Q
���i�|�P�Q�j�{�i�{�P�O�j
���|�Q
����ɂ���āA���ۂ̍��v�́A��̐����̍��v�����Q���������Ƃ��킩��
���������āA��ɂ������v���z800�~����i�|�Q�j����
800�{�i�|�Q�j��798
���v���z��798�~�ɂȂ�
�����̐����g�����֗��Ȍv�Z�i���ρj
�T�l�̕��ς����߂�
| A |
B |
C |
D |
E |
| �P�V�O |
�P�U�T |
�P�V�S |
�P�V�Q |
�P�U�S |
���ʂ̌v�Z�̂����ł́@�E�E�E�@
�i�P�V�O�{�P�U�T�{�P�V�S�{�P�V�Q�{�P�U�S�j���W�S�T�@�E�E�E�@�S���̍��v���v�Z����i�v�Z����ρj
�W�S�T���T���P�U�X�@�E�E�E�@�Ō�ɍ��v��l���ł���ĕ��ς��o��
�������̐����g����������
A�̂P�V�O����ɂ��āAB�AC�AD�AE����̒l���ǂꂾ���傫�������������𐳕��̐��ŕ\���Ă݂�ƁA
�@B�͊��170�����T����������i�|�T�j�ƕ\����B
�@C�͊��170�����S�傫������i�{�S�j�ƕ\����B
�@D�͊��170�����Q�傫������i�{�Q�j�ƕ\����B
�@E�͊��170�����U����������i�|�U�j�ƕ\����B
|
A |
B |
C |
D |
E |
| ���Ƃ��Ƃ̐� |
�P�V�O |
�P�U�T |
�P�V�S |
�P�V�Q |
�P�U�S |
| A����ɂ���� |
�O |
�|�T |
�{�S |
�{�Q |
�|�U |
�܂��A�����̐��ŕ\�������̂̍��v���v�Z����
�@ �O�{�i�|�T�j�{�i�{�S�j�{�i�{�Q�j�{�i�|�U�j
���i�|�T�j�{�i�|�U�j�{�i�{�S�j�{�i�{�Q�j
���i�|�P�P�j�{�i�{�U�j
���|�T
�@����ɂ���āA���ۂ̍��v�́A��̐����̍��v�����T���������Ƃ��킩��
�����l���ł��i���ς������j
�|�T���T���|�P
�@����ɂ���āA��̒l���ǂꂾ���傫��������������\�������̂̕��ς́A��̒l�����P���������Ƃ��킩��
��ɂ������ɂ��̐�������
�@ �P�V�O�{�i�|�P�j
���P�V�O�|�P
���P�U�X�@�E�E�E�@����ŕ��ς����߂�ꂽ�i�����̐��Ɋ����Όv�Z�͊ȒP�j
�����̕��@�ŕ��ς����߂邱�Ƃ��ł��闝�R��
�@ �i�P�V�O�{�P�U�T�{�P�V�S�{�P�V�Q�{�P�U�S�j���T�@�E�E�E�@�ʏ�̌v�Z��
���o�P�V�O�{�i�P�V�O�|�T�j�{�i�P�V�O�{�S�j�{�i�P�V�O�{�Q�j�{�i�P�V�O�|�U�j�p���T
���o�i�{�P�V�O�j�{�i�{�P�V�O�j�{�i�|�T�j�{�i�{�P�V�O�j�{�i�{�S�j�{�i�{�P�V�O�j�{�i�{�Q�j�{�i�{�P�V�O�j�{�i�|�U�j�p���T
���o�i�{�P�V�O�j�{�i�{�P�V�O�j�{�i�{�P�V�O�j�{�i�{�P�V�O�j�{�i�{�P�V�O�j�{�i�|�T�j�{�i�{�S�j�{�i�{�Q�j�{�i�|�U�j�p���T
���o�P�V�O�~�T�{�i�|�T�j�{�i�{�S�j�{�i�{�Q�j�{�i�|�U�j�p���T
���P�V�O�~�T���T�{�o�i�|�T�j�{�i�{�S�j�{�i�{�Q�j�{�i�|�U�j�p���T
���P�V�O�{�o�i�|�T�j�{�i�{�S�j�{�i�{�Q�j�{�i�|�U�j�p���T
���i��ɂ������j�{�i��������Ƃɐ����̐��ŕ\�������̂̕��ρj
|